5.2.6 Heat generation caused by electrical current

For coupled thermal-electrical and coupled thermal-electrical-structural analyses in Abaqus/Standard the user can introduce a factor, 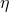 , which defines the fraction of electrical dissipation in the contact zone converted to heat. The fraction of generated heat into the first and second surface,
, which defines the fraction of electrical dissipation in the contact zone converted to heat. The fraction of generated heat into the first and second surface, 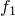 and
and 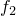 , respectively, can also be defined.
, respectively, can also be defined.
The heat fraction, 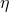 , determines the fraction of the energy dissipated due to electrical current that enters the contacting bodies as heat. Heat is instantaneously conducted into each of the contacting bodies depending on the values of
, determines the fraction of the energy dissipated due to electrical current that enters the contacting bodies as heat. Heat is instantaneously conducted into each of the contacting bodies depending on the values of 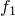 and
and 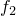 . The contact interface is assumed to have no heat capacity and may have properties for the exchange of heat by conduction and radiation.
. The contact interface is assumed to have no heat capacity and may have properties for the exchange of heat by conduction and radiation.
The heat flux densities, 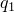 , going out the surface on side 1, and
, going out the surface on side 1, and 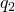 , going out the surface on side 2, are given by
, going out the surface on side 2, are given by
and
where
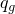
is the heat flux density generated by the interface element due to electrical current,
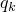
is the heat flux due to conduction, and
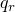
is the heat flux due to radiation.
The heat flux due to conduction is assumed to be of the form
where the heat transfer coefficient
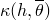
is a function of the average temperature at the contact point,
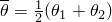
, and overclosure,
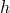
.
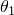
and
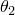
are the temperatures of side 1 and side 2, respectively.
The heat flux due to radiation is assumed to be of the form
where
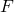
is the gap radiation constant (derived from the emissivities of the two surfaces) and
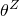
is the absolute zero on the temperature scale used.
The electrical flux density, 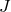 , in the interface element is given in terms of the difference in the electric potential,
, in the interface element is given in terms of the difference in the electric potential, 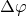 , across the interface:
, across the interface:
where the gap electrical conductance
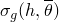
is a function of the overclosure,
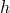
, and the average temperature at the contact point,
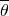
.
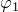
and
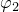
are the electric potentials of side 1 and side 2, respectively.
In a steady-state analysis the heat flux density generated by the interface element due to electrical current is given by
where
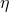
is the fraction of dissipated energy converted to heat. In a transient analysis the average heat flux density is given by
where
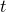
is the time at the start of an increment and
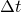
is the time increment.
Using the Galerkin method, the weak form of the equations can be written as
The contribution to the variational statement of thermal equilibrium is
where
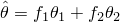
. The contribution to the Jacobian matrix for the Newton solution is
At a contact point the temperatures can be interpolated with
where
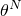
is the temperature at the
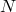
th node associated with the interface element. Note that the summation convention will be used for all superscripts. Therefore, the temperature variables can be written as follows:
where
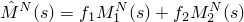
and
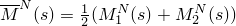
. Substituting the above expressions to
Equation 5.2.6–1, we obtain
The derivatives of
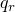
,
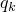
, and
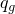
, are as follows:
and in a steady-state analysis
while in a transient analysis
Similarly, the contribution to the variational statement of electrical equilibrium is
and the contribution to the Jacobian matrix for the Newton solution is
The derivatives of
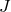
are

![]() , which defines the fraction of electrical dissipation in the contact zone converted to heat. The fraction of generated heat into the first and second surface,
, which defines the fraction of electrical dissipation in the contact zone converted to heat. The fraction of generated heat into the first and second surface, ![]() and
and ![]() , respectively, can also be defined.
, respectively, can also be defined.![]() , determines the fraction of the energy dissipated due to electrical current that enters the contacting bodies as heat. Heat is instantaneously conducted into each of the contacting bodies depending on the values of
, determines the fraction of the energy dissipated due to electrical current that enters the contacting bodies as heat. Heat is instantaneously conducted into each of the contacting bodies depending on the values of ![]() and
and ![]() . The contact interface is assumed to have no heat capacity and may have properties for the exchange of heat by conduction and radiation.
. The contact interface is assumed to have no heat capacity and may have properties for the exchange of heat by conduction and radiation.![]() , going out the surface on side 1, and
, going out the surface on side 1, and ![]() , going out the surface on side 2, are given by
, going out the surface on side 2, are given by ![]()
![]()
![]()
![]()
![]() , in the interface element is given in terms of the difference in the electric potential,
, in the interface element is given in terms of the difference in the electric potential, ![]() , across the interface:
, across the interface: ![]()
![]()
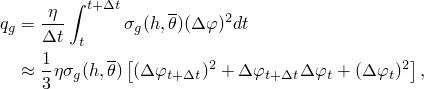
![]()
![]()
![]()
![]()
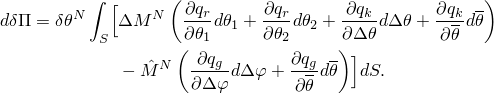
![]()
![]()
![]()
![]()
![]()
![]()
![]()