Product: Abaqus/CFD
Time accuracy, laminar flow, surface output, time-history data, spatial and temporal accuracy.
Two-dimensional laminar flow over a cylinder is a well-documented fluid dynamics problem, which makes it suitable for verification. This problem is characterized by boundary layer separation resulting from adverse pressure gradients induced by the cylinder geometry. The flow is characterized by a Reynolds number, 
, defined with a free-stream velocity, V, and cylinder diameter, D, where 
and 
are the dynamic viscosity and density of the fluid, respectively. At sufficiently high Reynolds number, 
, the flow becomes unsteady and is characterized by vortices shed from either side of the cylinder in an alternating manner. The resulting downstream wake pattern is known as a Karman vortex street. The frequency at which the vortices are shed is characterized by a nondimensional parameter known as the Strouhal number 
, where f is the vortex shedding frequency. Experimental studies have demonstrated that the Strouhal number is Reynolds number dependent (Roshko, 1954), indicating that, despite the simple geometry, the flow is far from being simple.
This problem was selected as an Abaqus/CFD verification problem because of the simple geometry, the unsteady dynamics, and the availability of experimental and numerical results for comparison. Specifically, we consider the case of 
flow as the benchmark problem for which the Strouhal number, 
, is obtained from the experimental data using the correlation formula given by Roshko, 1954. The objective of the study is to reproduce the unsteady structure of the flow and to measure the convergence rate of Abaqus/CFD.
Model:
The model consists of a two-dimensional cylinder in a rectangular domain, as shown in Figure 3.3.1–1. The inflow boundary is located 8D upstream of the cylinder axis, the outflow boundary surface is located 25D downstream of the cylinder axis, and the top and bottom surfaces are located 8D away from the cylinder axis. The thickness of the cylinder is 0.2D in the spanwise direction.
Mesh:
The domain topology (see Figure 3.3.1–2) is partitioned into two regions: the cylinder region—which is the box bounded by 
and 
with the origin located at the center of the cylinder (circle)—and the far field and wake region that cover the complement of the domain.
In this study five meshes with varying element sizes, summarized in Table 3.3.1–1, are employed. Mesh refinement is performed uniformly all over the computational domain (see Figure 3.3.1–3). To measure the mesh refinement, a mesh metric h (from ASME V V 20-2009) is used to compare results among meshes:
denotes the volume of a given element i, and 
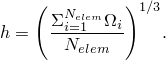
is the number of elements in the mesh.Table 3.3.1–1 Mesh description.
| Mesh | Number of elements | h/D |
|---|---|---|
| 1 | 2,520 | 0.3471 |
| 2 | 4,068 | 0.2959 |
| 3 | 5,902 | 0.2614 |
| 4 | 7,630 | 0.2399 |
| 5 | 10,080 | 0.2187 |
Boundary conditions:
The boundary conditions applied to the model are shown schematically in Figure 3.3.1–4.
At the inflow surface (
) the fluid velocity is specified in component form as (
) = (V, 0, 0). At the top and bottom surfaces (
) a tow-tank velocity condition is specified as () = (V, 0, 0). At the outflow surface (
) an outflow boundary condition (traction free) is specified by setting the pressure p = 0 (the gradients of velocities are automatically set to zero for this boundary). On the cylinder surface (
) a no-slip/no-penetration boundary condition is enforced, given by () = (0, 0, 0). Finally, the two-dimensional nature of the problem is enforced by prescribing the out-of-plane velocity, 
, to be zero everywhere on the domain surface and by using only one element through the thickness along the cylinder axis. Initial conditions:
The velocity, V, is set to zero everywhere in the flow domain. Velocity initial conditions that satisfy the solvability conditions for the incompressible Navier-Stokes equations are obtained by inserting the boundary conditions in the prescribed initial velocity field, followed by a projection to a divergence-free subspace. This mass adjustment to the velocity initial conditions is necessary to guarantee that the flow problem is well posed.
Problem setup:
The fluid density, cylinder diameter, inflow velocity, and dynamic viscosity values are specified as = 1 kg /m3, D = 1 m, V = 1 m/s, and = 0.01 kg/ms, respectively. These values yield a Reynolds number of 100. Transient flow simulations using a fixed step size of 
and total simulated time t = 350 s are conducted for all meshes. The fixed 
used is smaller than the computed using a fixed 
number for all meshes. A time weight of 
is used for the diffusion and advective terms; and the solver options are set to the defaults with the exception of the pressure Poisson equation (PPE) solver tolerance, which is set to 10–8 (default 10–5).
This verification study is intended to assess the time accuracy of Abaqus/CFD for a 
flow where a Hopf bifurcation results in steady, periodic vortex shedding. Experimental data and well-established numerical calculations are used as benchmark solutions to compare with the results obtained here.
The time at which vortex shedding first develops depends on the mesh quality. For all meshes used in this study, a periodic vortex shedding system is fully established around 225 time units, after which numerical calculations were conducted for a period of 125 time units to collect time-history data for the drag coefficient (
), the lift coefficient (
), and the velocity (
) for all meshes. The time history signals were analyzed using a numerical discrete Fast Fourier Transform to extract the dominant frequency. For this moderate 
case there is only one dominant frequency (corresponding to the Hopf bifurcation) that can also be computed directly by counting the number of zero crossings during the time sample. Both approaches yielded effectively the same results.
Figure 3.3.1–5 indicates the four locations, 
= (4, 8, 12, 16) approximately, and 
above the centerline, marked in red, where the time history of y-velocity is collected for Mesh 5.
coefficient for Mesh 5: the results show the progressive increase in lift followed by the steady state reached once the vortex shedding dynamics are established. The computed average lift coefficient is equal to 0. Figure 3.3.1–8 shows a 50-second span of the time history data for Mesh 5 and reveals the periodic variation in drag induced by the vortex shedding. The frequency of a vortex-shedding cycle is equal to one-half of the frequency of the drag signal. Results for the rest of the meshes exhibit the same behavior; thus, these results are not presented here. To compute the vortex shedding frequency, the spectrum of the drag coefficient is calculated as
is the Fourier transform of the drag coefficient and 
is its complex conjugate. The drag coefficient is defined as
is the drag force (integrated force in the direction of the flow) and b is the spanwise dimension of the cylinder. Figure 3.3.1–9 shows the spectrum versus Strouhal number computed for Mesh 5, which indicates that the dominant frequency is located at 
.Following the same procedure, the Strouhal numbers computed for all meshes employed in this study are summarized in Table 3.3.1–2.
Table 3.3.1–2 Calculated Strouhal number.
| Mesh | |  | Number of samples per period  |
|---|---|---|---|
| 1 | 0.01 | 0.1559 | 641 |
| 2 | 0.01 | 0.1639 | 610 |
| 3 | 0.01 | 0.1639 | 610 |
| 4 | 0.01 | 0.1679 | 600 |
| 5 | 0.01 | 0.1679 | 600 |
. Table 3.3.1–3 Calculated Strouhal number from benchmark calculations (Engelman and Jamnia, 1990).
| Mesh | | | Number of samples per period |
|---|---|---|---|
| Coarse | 0.269 | 0.172 | 22 |
| Medium | 0.264 | 0.172 | 22 |
| Fine | 0.266 | 0.173 | 22 |
To further assess the spatial accuracy of the code, the mean drag coefficient obtained by averaging the time signal is used with a Richardson extrapolation to estimate the convergence rate. Results are summarized in Table 3.3.1–4, and Figure 3.3.1–10 shows the convergence of the drag coefficient as a function of the mesh metric (h) . In addition, the benchmark solution taken from Engelman and Jamnia, 1990 is presented in Table 3.3.1–5.
Table 3.3.1–4 Calculated mean drag coefficient.
| Mesh | h/D |  |
|---|---|---|
| 1 | 0.3471 | 1.3848 |
| 2 | 0.2959 | 1.4000 |
| 3 | 0.2614 | 1.4065 |
| 4 | 0.2399 | 1.4078 |
| 5 | 0.2187 | 1.4105 |
Table 3.3.1–5 Calculated mean drag coefficient from benchmark calculations (Engelman and Jamnia, 1990).
| Mesh | h/D | |
|---|---|---|
| Coarse | 0.7791 | 1.405 |
| Medium | 0.6930 | 1.410 |
| Fine | 0.6128 | 1.411 |
The rate of spatial convergence of Abaqus/CFD can be estimated using the results of the four meshes. Following ASME V V 20-2009, the error in the numerical solution can be computed as
, is obtained as
, such that 
= 1.4207. This value is close to the experimental data of 
= 1.422 reported by Wieselsberger, 1922. Hence, the experimental drag coefficient is used to calculate the error in the calculations. Figure 3.3.1–11 presents the absolute value of the error for the drag prediction. Results indicate that error decays with a rate consistent with the second-order spatial accuracy of Abaqus/CFD, illustrated by the line with slope 
that is plotted on top of the results. However, the nonmonotonicity of the convergence rate is caused by a lack of control in the mesh generation process. It was not always possible to refine all the regions of the mesh consistently, especially in the cylinder region, which slightly affects the mesh metric h and consequently affects the convergence rates.Following ASME V V 20-2009, the observed convergence between two calculations can be approximated as
and 
, with 
. Table 3.3.1–6 shows the convergence rate computed using the equation above. The unsteady incompressible flow over a cylinder was successfully computed using Abaqus/CFD. The vortex shedding frequencies computed were found to be in good agreement with the experimental data and previous numerical calculations. Furthermore, the estimated overall convergence rate for the Abaqus/CFD drag coefficient was measured and was found to be in close agreement with the theoretical second-order accuracy of the code.
Mesh 1: Mesh with 2520 elements.
Mesh 2: Mesh with 4068 elements.
Mesh 3: Mesh with 5902 elements.
Mesh 4: Mesh with 7630 elements.
Mesh 5: Mesh with 10080 elements.
ASME V V 20-2009, “Standard for Verification and Validation in Computational Fluid Dynamics and Heat Transfer,” American Society of Mechanical Engineers.
Engelman, M. S., and M. A. Jamnia, “Transient Flow Past a Circular Cylinder: A Benchmark Solution,” International Journal for Numerical Methods in Fluids, vol. 11, pp. 985–1000, 1990.
Roshko, A., “On the Development of Turbulent Wakes from Vortex Streets,” National Advisory Committee for Aeronautics, Washington, D. C., Report 1191, 1954.
Wieselsberger, C., “New Data on the Laws of Fluid Resistance,” NACA-TN-84, 1922.
